Rozpočtová položka a jej vlastnosti

2024 Autor: Howard Calhoun | [email protected]. Naposledy zmenené: 2024-01-02 14:02

V názve - jeden zo základných pojmov teórie spotrebiteľského správania. Čo je rozpočtový riadok? Ide o graf, ktorý pomáha analyzovať možnosti, túžby spotrebiteľa. Povedzme si podrobnejšie o koncepte, vlastnostiach objektu, ako aj o súvisiacich pojmoch a javoch.

Definícia slova

Rozpočtová čiara (BL) je priama čiara, ktorej body znázorňujú súbory tovarov, na ktoré sa pridelený rozpočet minie v plnej výške. Pretína súradnicové osi Y a X v bodoch, ktoré označujú najväčší možný počet produktov, ktoré je možné zakúpiť za konkrétny príjem za súčasné ceny.

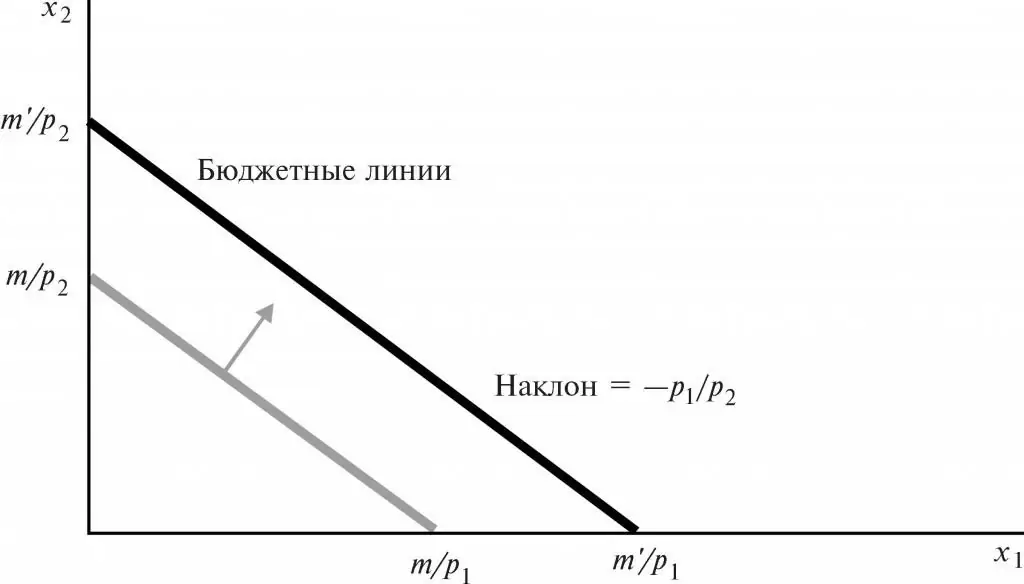
BL teda predvádza rôzne kombinácie 2 sád akéhokoľvek tovaru, ktorý sa kupuje za určitý zisk a pevnú cenu.

BL vlastnosti

Predstavme si vlastnosti rozpočtových riadkov.

1. Majú len negatívny sklon. Keďže sady tovarov nachádzajúce sa v BL majú rovnaké ceny, zvýšenie počtu nákupov jedného vedie k zníženiu nákupov druhého. Pripomeňme, že krivka zobrazujúca spätnú väzbu medzi dvoma premennými má vždy záporný sklon.

2. Umiestnenie základňovej stanice závisí od hodnoty zisku spotrebiteľa. Ak sa jeho príjem zvýši a ceny zostanú rovnaké, rozpočtový riadok sa posunie doprava, paralelne s predchádzajúcim riadkom. Ak zisk klesá pri stálych cenách, potom BL ide doľava, ale stále paralelne so starou čiarou.

Zmena príjmu spotrebiteľa teda nepovedie k zmene uhla sklonu BL. Menia sa iba body jeho priesečníka so súradnicovými osami X a Y.

3. Koeficient sklonu BL sa rovná pomeru nákladov na ekonomický tovar s opačným znamienkom. Vysvetlime si túto vlastnosť. Koeficient sklonu BL je pomer ceny produktu meranej horizontálne k cene produktu meranej vertikálne. Preto strmosť tohto sklonu: P_x /P_{y(cena produktu X, cena produktu Y).}

Znamienko "mínus" v tomto prípade označuje záporný sklon BL (napokon, ceny produktov X a Y budú vždy len kladné hodnoty). Odtiaľto sa musíte zdržať nákupu niektorých položiek z komplexu X, aby ste si kúpili niečo zo sady Y.

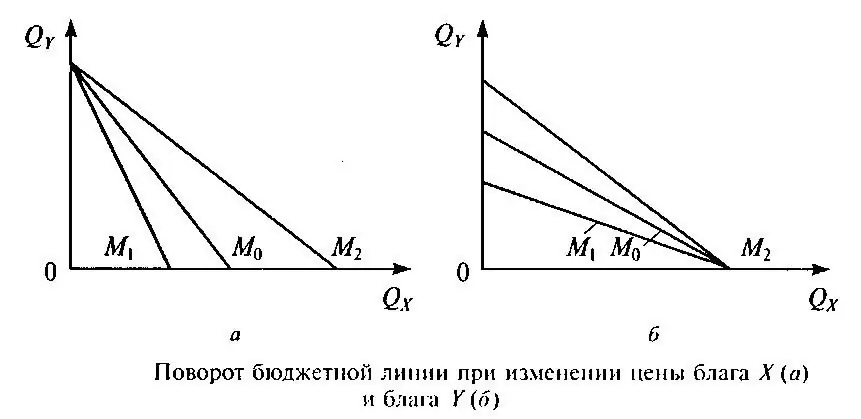
4. Zmena cien ekonomických tovarov ovplyvňuje zmenu sklonu BL. Tu vidíme nasledovné. Ak sa zmenia náklady na jeden produkt, zmení sa uhol sklonu rozpočtovej línie a umiestnenie jedného z priesečníkov BL so súradnicovou osou.

Ak sa však ceny oboch tovarov líšia, potom sa to rovná zmene veľkosti celkového zisku spotrebiteľa. To znamená, že BL sa v tomto prípade posunie doprava alebo doľava.

Rozpočtový strop

Rozpočtový riadok je prepojený so širšími konceptmi. Prvým je rozpočtové obmedzenie. Sú to všetky súbory tovarov, ktoré si spotrebiteľ môže kúpiť za určitý rozpočet a aktuálne ceny. Zákon rozpočtového obmedzenia: Celkový príjem sa rovná celkovým výdavkom. Pri akejkoľvek zmene výšky zisku sa rozpočtový riadok posunie.

Obmedzenie rozpočtu možno opísať rovnicou: P_xQ_x + P_y Q y _{≦ M. Dešifrovať:}

• P_x, P_{y – cena dvoch tovarov (X a Y).}
• Q_x, Q_{y – určité množstvo tovaru X a Y.}
• M je rozpočet, ktorý má spotrebiteľ k dispozícii.
• Znamienko „menej alebo rovné“znamená, že celková suma výdavkov nemôže byť vyššia ako príjem osoby. Maximálne výdavky sa môžu rovnať celkovému zisku.

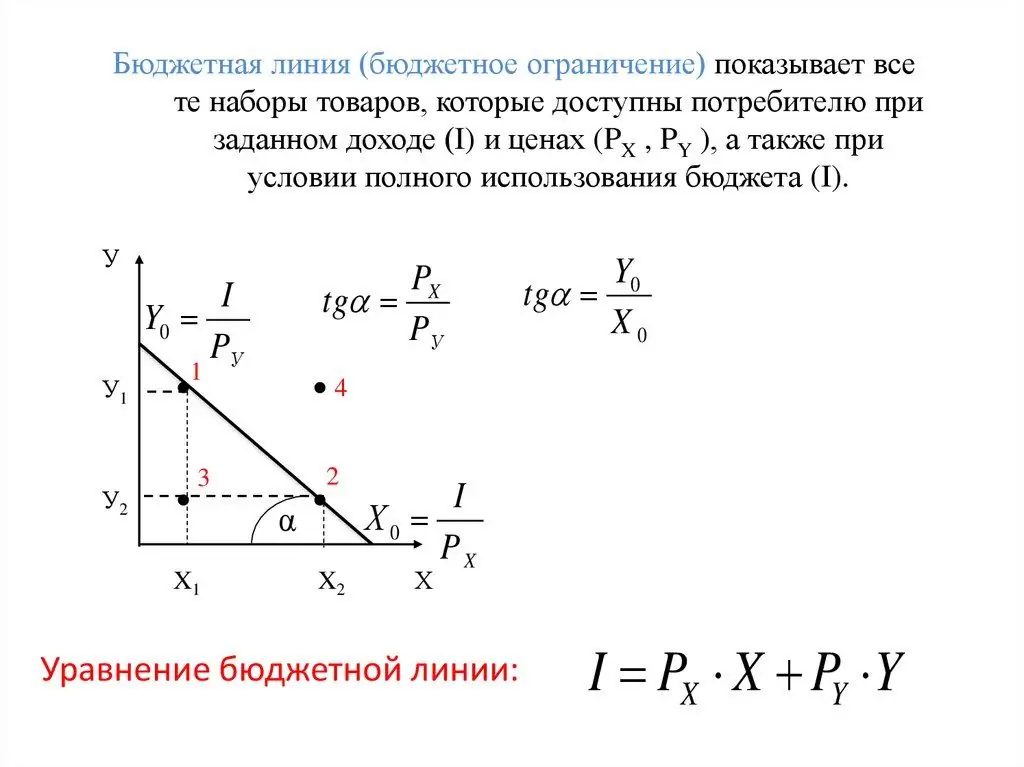
Odtiaľto je jasné, ako BL pretína súradnicové osi X a Y v dvoch bodoch:

• X₁ =M/P_x.
• Y₁ =M/P_y.

Tieto body v rozpočtovom riadku zobrazujú maximálne množstvo produktov X a Y, ktoré je možné zakúpiť za príjem spotrebiteľa za dnešné ceny.

Fiškálny priestor

Ďalším dôležitým súvisiacim konceptom je rozpočtový priestor. Toto je názov celej výberovej zóny dostupnej pre spotrebiteľa. Na grafoch je znázornený tieňovaným trojuholníkom. Na jednej strane je limitovaný rozpočtovou líniou spotrebiteľa, na druhej strane súradnicovými osami X resp. W.

Na výber takéhoto priestoru na obrázku stačí zostrojiť priamku rozpočtového obmedzenia pomocou vzorca: P_xQ_{x+ P} y_Qy_=M.

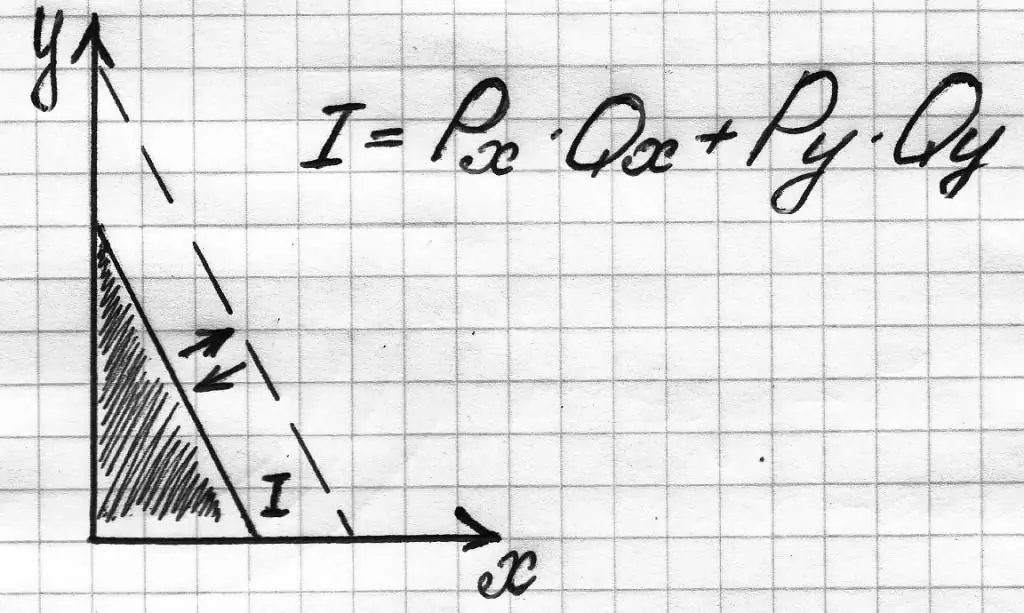
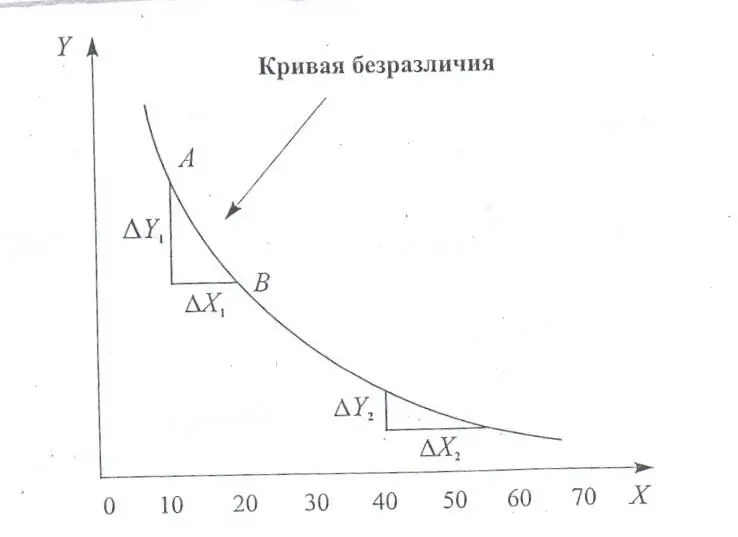
Indiferenčná krivka

Indiferenčná krivka (indiferenčná krivka) – ide o rôzne kombinácie dvojice ekonomických výhod, ktoré sú pre človeka rovnako potrebné. Pomocou takýchto grafov sa dá ukázať rovnováha spotrebiteľa – bod maximalizácie celkového úžitku, spokojnosť z míňania fixného zisku.

Indiferenčné krivky sú široko používané nástroje neoklasickej ekonomickej školy. Najmä sú použiteľné pri štúdiách mikroekonomických situácií súvisiacich s problémom voľby.

Vlastnosti indiferenčných kriviek (IB) sú nasledovné:

• CB má vždy negatívny sklon, pretože racionálni spotrebitelia uprednostňujú viac ako menej.
• CB vyššie a napravo od druhej krivky preferuje spotrebiteľ.
• CB majú konkávny tvar – je určený hraničnými klesajúcimi mierami substitúcie.
• Komplexy tovaru na krivkách, ktoré sú vzdialenejšie od začiatku súradníc, sú vhodnejšie ako sady na krivkách X a Y osiach bližšie k nule.
• CB sa nemôžu prekrývať. Ukazujú okrajové klesajúce miery nahradenia jedného produktu iným.

Komplex CB tvorí mapu súboru indiferenčných kriviek. Používa sa na opis spotrebiteľských preferencií pre všetky druhy ekonomických tovarov.

Indiferenčné krivky a rozpočtová línia

Ako spolu tieto pojmy súvisia? Krivka ľahostajnosti ukazuje, čo by si človek chcel kúpiť. A BL - čo môže dostať. Spoločne odpovedajú na otázku: „Ako môžete získať čo najväčšiu spokojnosť z nákupu s obmedzeným ziskom?“

CB a BL sa teda používajú na grafické znázornenie situácie, kedy človek maximalizuje úžitok, ktorý získa kúpou dvoch tovarov s obmedzeným rozpočtom. Odtiaľ je možné izolovať požiadavky optimálneho súboru spotrebného tovaru. Sú len dve z nich:

• Nájdenie skupiny tovaru na krivke rozpočtovej línie.
• Poskytovať spotrebiteľovi najvýhodnejšiu kombináciu.

Rozpočtový riadok teda pomáha predstaviť si pomery, v ktorých je možné zakúpiť dva rôzne súbory ekonomického tovaru za pevný rozpočet. Tento graf sa často analyzuje spolu s indiferenčnou krivkou a inými súvisiacimi javmi.